13.3. Gradient Balance

In curved flow, geostrophic balance does not apply because of the addition of the centrifugal force. Therefore, the gradient wind balance is a three-way balance between the pressure gradient force, Coriolis force, and the centrifugal force (Fig. 13.3). This balance applies in upper-level troughs and ridges and can be written algebraically as,

\[ \begin{align}\begin{aligned} 0 = -\frac{1}{\rho}\frac{\Delta p}{\Delta x} + f V + \frac{V^2}{R}\\0 = -\frac{1}{\rho}\frac{\Delta p}{\Delta x} - f U + \frac{U^2}{R} \end{aligned}\end{align} \]

This equation can be solved using the quadratic formula. If the pressure gradient were equal around both a high and a low, gradient wind balance would dictate that winds around a high would be supergeostrophic (faster than the geostrophic balance would predict) and subgeostrophic (slower than the geostrophic balance would predict) around a low.

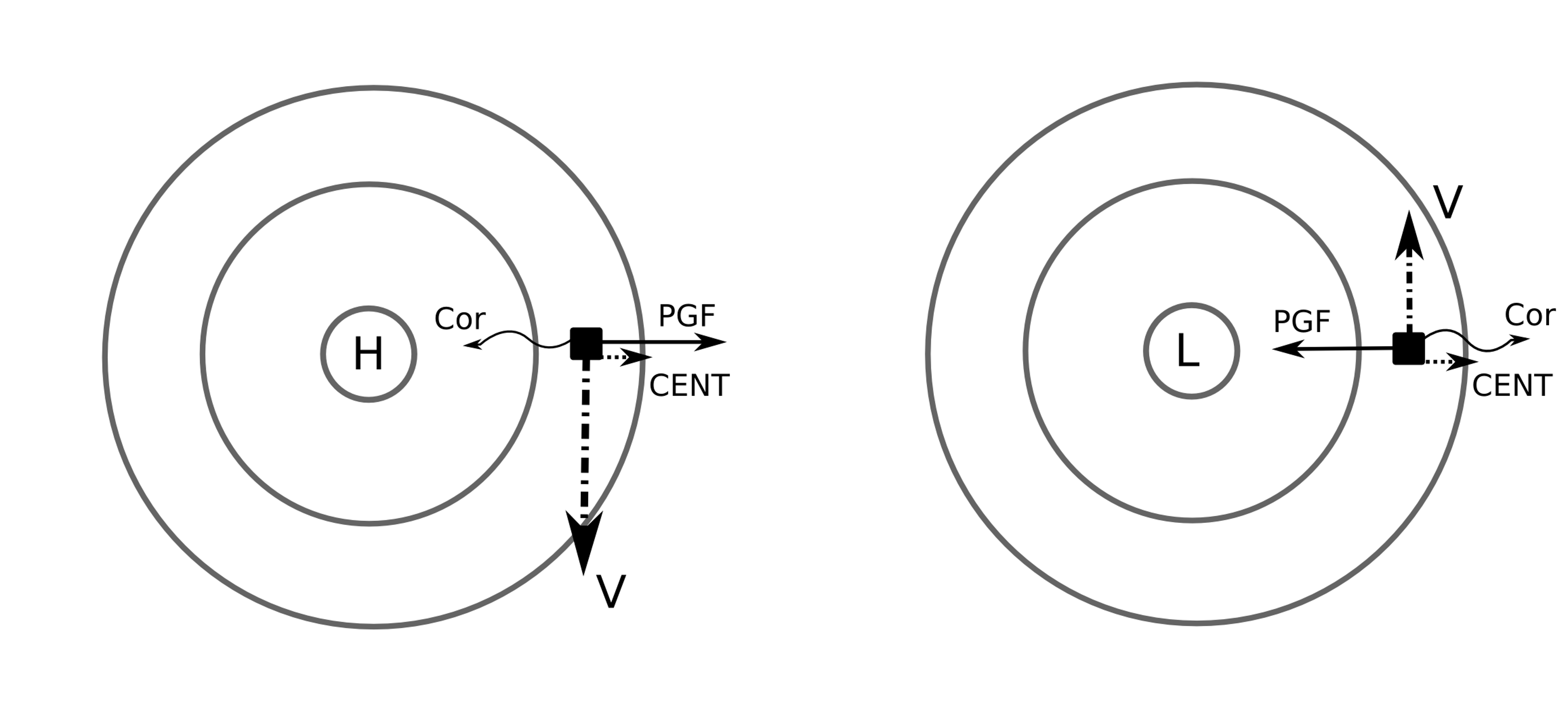
Fig. 13.3 A force balance diagram illustrating Gradient wind balance.

Note

When using the quadratic formula to solve for the gradient wind, to make it easier, you’ll want to think about how you can define your different values of a, b, and c from the prototypical quadratic formula.

If a typical quadratic equation can be written as,

\[a v^2 + b v + c = 0\]

then you can use the following quadratic formula to solve for v,

\[ v = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a} \]