11.1. Pressure Gradient Force#
There are a number of forces (accelerations) that govern atmospheric flows. The most important is the pressure gradient force (PGF). The PGF is the only force that can actually cause the wind to blow. All other forces act upon the already moving air in the atmosphere. Mathematically we can write a pressure gradient (PG) in algebraic form as,
where \(\Delta p\) is a change in pressure and \(\Delta n\) is a change in distance. This is not quite our pressure gradient force. Pressure has units of \(N\) \(m^{-2}\), which is force per unit area, whereas the PG has units of \(N\) \(m^{-3}\), which is a force per unit volume. To get it into our pressure gradient force that we use in meteorology we need to divide by density, \(\rho\):
By convention, we place the negative sign in front of the PGF so that the force always points toward low pressure where the units of PGF are \(m\) \(s^{-2}\) (an acceleration). Air will ALWAYS move from higher pressure to lower pressure.
Looking at this concept graphically we can inspect a 500-hPa plot of geopotential heights (Fig. 11.1). Where lines of geopotential height are closest together indicates where the strongest height gradients are located. In figure 11.1, we can see that the red dashed contours are located where the black geopotential height contours are most closely packed, thus indicating the areas on this particular map where the strongest height gradients are located.
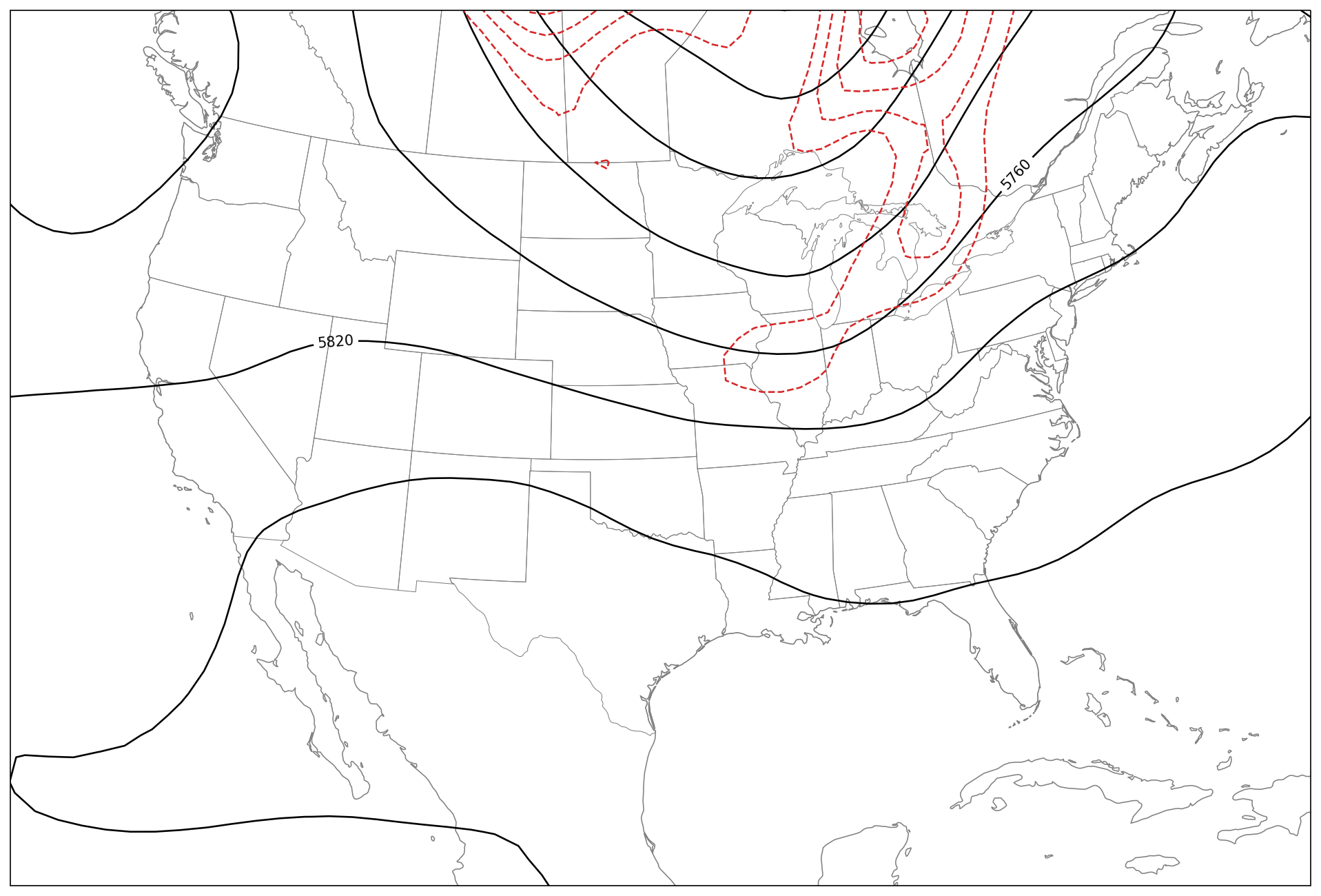
Fig. 11.1 This map shows 500-hPa heights in solid black contours and the magnitude of the height gradient in dashed red contours.#
